by Alexandra Bakman
How can we understand the behavior of the atmospheric currents and the flow of the water exiting a tap? What is the information encoded in the motion of microscopic particles and how can we read it? These and other questions are the research focus of Prof. Anna Frishman, a new member of the physics faculty at the Technion.
What is the connection between entropy production and transmission theory? How can we analyze the currents occurring in the atmosphere?
Across the years, physicists have pondered over various phenomena, searched for connections between them and ways to explain one by using the other, and the curiosity never faded.
This time, we will take a glimpse into the scientific world of Prof. Anna Frishman, a new faculty member at the Physics faculty at the Technion. Her research topics include turbulence and non-equilibrium statistical physics.
Prof. Frishman studied in Weizmann for her MSc and PhD degrees and conducted her Post-Doctoral research at Princeton University. Her common themes across the various degrees were fluid dynamics and out-of-equilibrium statistical mechanics, with turbulence at the intersection.
When we think about turbulence, we should remember it is a regime present in many aspects of our lives, from turbulence experienced during airplane flight and the fast flow coming out of the tap to smoke rising from a cigarette.
It is a regime of flow with a high Reynolds number, which means that, at most scales, the inertia in the flow is more important than dissipation. This fact leads to a high velocity flow that appears random in time and space. For example, the rapid flow of a river consists of the average current with random fluctuations on top. Turbulence also occurs when the flow encounters an obstacle, such as a stone or a stray plastic bottle. Despite being ubiquitous, and thus the subject of intensive research for more than a century, turbulence still has many more open questions than answers; One of the main difficulties is that a complete description requires developing a theoretical framework for a strongly interacting out-of-equilibrium field theory.
Apart from three dimensional systems, turbulence can also exist in two dimensions, or layers that we can assume to be two dimensional – for example, large scale flows in the atmosphere are quasi-two dimensional: their extent is much larger than the depth of the atmospheric layer. However, the behavior of turbulence in two dimensions is surprisingly different.
In three dimensions, turbulence takes energy from large scale flows and transfers it into smaller eddies, and from these eddies into even smaller ones. This process ends when energy reaches small enough scales where dissipation is efficient. However, in two dimensions, the eddies join forces instead. This effect, called an inverse cascade, discovered by Robert Kraichnan, tells us that turbulence in a flattened fluid passes energy into bigger, not smaller, scales. As a result, a large, stable flow is formed.
In her postdoctoral studies, Prof. Frishman studied this effect of the self organization of random fluid excitations. If the friction with the bottom of the container in which the fluid is located is substantially reduced, eventually a large coherent flow is formed. It was plausible to assume that the characteristics of this flow do not depend on the specific properties of the forces which excite the fluid at small scales. In her research, Prof. Frishman helped develop a theory which explained how this large scale flow is determined self-consistently, as well as the nature of the small fluctuations of the fluid which coexist
with it. This is the first-ever self-consistent theory of the interaction between turbulence and a coherent flow. Extending it to three dimensional flows, to encompass flows in pipes or the atmospheric boundary layer for example, remains a challenge for the future, with huge practical implications.
Another topic, on which Prof. Frishman worked in her postdoctoral research, and which extends into her current work, is the study of overdamped particle dynamics in the presence of noise from the environment. In the overdamped regime, the friction with the solution is much greater than particle inertia, which is typically the case at small scales, corresponding to a low Reynolds number.
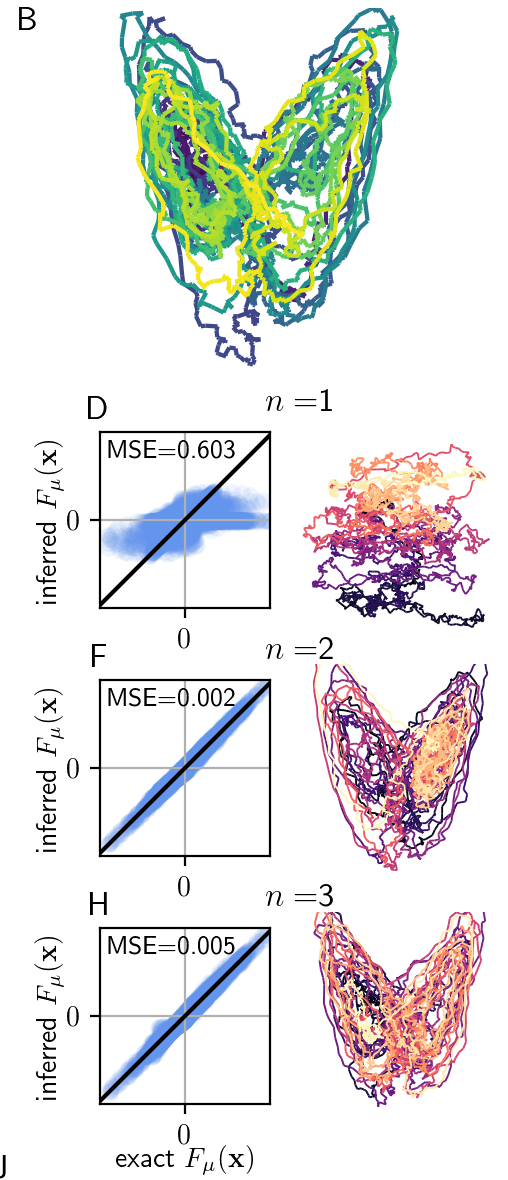
For example, for particles at the micron scale and below, the thermal fluctuations they feel are important. Indeed, the collisions with the molecules in the solution translate to a random white force, causing the particles to perform Brownian motion in the absence of other forces. Thus, other forces acting on the particles, which could result from interactions between particles or from an external field, are always obscured by the random forces. The research question was whether these deterministic forces could be deduced solely from the trajectories of the particles.
More generally, such dynamics is called Brownian dynamics and is a basic model for the dynamics of systems with fast, unresolved degrees of freedom, modeled as the white noise. Indeed, this model is commonly used in finance, climate dynamics and biology.
Prof. Frishman drew a parallel between systems of this kind and transmission theory, where a signal is encoded, then transmitted through a noisy channel and eventually read by a recipient. In our case, the message is the force, the encoding is the measurement of this force along the trajectory, and the noise from the channel is the white noise added to the force.
Prof. Frishman developed a framework which enabled to deduce this force, using the notion that for any finite trajectory there exists a finite amount of information. The framework consists of a smooth regression of the force field with known functions, where both under- and over-fitting are controlled based on the information in the decomposition. The analogue between dissipation in these systems and transmission theory was a novel and conceptually interesting idea.
Ronceray and Frishman, PRX (2020)
This framework could prove useful to scientists performing experiments on active particles with internal driving as well as interparticle interactions. More generally, it could be used on a broad class of stochastic systems where inferring a dynamical model from limited noisy data is of interest.
Broadly, Prof. Frishman is interested in problems combining nonlinear dynamics and statistics. Her overarching goal is to find whether there are guiding principles, or a mathematical formalism to describe out of equilibrium systems, and in particular the goal to better understand the role of the dynamics in them. The prominent applications of such an understanding are turbulent flows and biological systems.
And of course, being a scientist means not only being a dreamer but also being curious about daily phenomena.
To prove this point, Prof. Frishman is also interested in the non-linear dynamics of a cylindrical soap bubble, which while being pulled to the sides, pops and creates a small bubble in the middle. The research question is, how is the size of this small bubble connected to the pull velocity, taking into account the flow inside the bubble and surface tension.

The world of non-equilibrium dynamics and turbulence is a fascinating one, and full of open questions. The journey to find answers never ends, and you are most invited to join it.