כתבה: אלכסנדרה בקמן
כיצד אפשר להבין את התנהגות הזרמים באטמוספירה ואת תנועת המים שיוצאים מהברז? איזה מידע על הסביבה מקודד בתנועה של חלקיקים מיקרסוקופיים וכיצד ניתן לקרוא אותו? שאלות אלו ואחרות מעסיקות את פרופ' פרישמן, חברה חדשה בפקולטה לפיזיקה בטכניון.
מה הקשר בין ייצור אנטרופיה ותורת הממסר? כיצד נוכל לנתח את הזרמים שנוצרים באטמוספירה?
במרוצת השנים, שקדו פיסיקאים על מציאת הסבר לתופעות השונות, וחיפשו את הקשרים ביניהן וכן דרכים להסביר תופעה אחת באמצעות תופעה אחרת, והסקרנות לעולם לא פחתה.
הפעם נציץ אל עולמה המדעי של פרופ' אנה פרישמן, חברה חדשה בפקולטה לפיסיקה בטכניון. נושאי המחקר שלה כוללים טורבולנציה ופיסיקה סטטיסטית מחוץ לשיווי משקל.
פרופ' פרישמן סיימה את לימודי המאסטר והדוקטורט שלה במכון ויצמן למדע וביצעה את מחקר פוסט הדוקטורט שלה באוניברסיטת פרינסטון. הנושאים המשותפים לכל שנותיה במחקר היו דינמיקת זורמים ומכניקה סטטיסטית מחוץ לשיווי משקל, עם טורבולנציה במפגש ביניהם.
כאשר אנו חושבים על טורבולנציה, יש לזכור כי התופעה קיימת במקומות רבים בחיינו, החל מטורבולנציה שמורגשת בטיסות, וכלה בזרימה חזקה של מים מהברז ועשן העולה מסיגריה דולקת.
זרימה טורבולנטית מתאפיינת במספר ריינולדס גבוה, כלומר, ברוב הסקאלות האינרציה של הזרימה משמעותית יותר מהדיסיפציה. התוצאה היא זרימה עם מהירות גבוהה שנראית אקראית בזמן ובמרחב. לדוגמה, זרימה מהירה של נהר מורכבת מזרימה ממוצעת עם תנודות אקראיות חלשות. כמו כן, טורבולנציה מתרחשת כאשר זרימה פוגשת מכשול, כמו אבן או בקבוק פלסטיק זרוק. למרות שתופעה זו נמצאת בכל מקום, ומהווה נושא מחקר במשך יותר ממאה שנים, עדיין כמות השאלות הפתוחות בנושא עולה על כמות התשובות. אחד הקשיים הוא שעל מנת לספק תיאור מקיף לתופעה, דרוש פיתוח מסגרת תיאורטית עבור תורת שדות מחוץ לשיווי משקל, הכוללת אינטרקציות חזקות.
חוץ ממערכות תלת מימדיות, טורבולנציה יכולה להתקיים גם בדו מימד, או שכבות שניתן לחשוב עליהן כעל דו מימדיות – למשל, זרימות בקנה מידה גדול באטמוספירה, אשר השטח שלהן גדול הרבה יותר מעומק השכבה האטמוספירית. עם זאת, התנהגות הטורבולנציה בדו מימד שונה באופן מפתיע מההתנהגות התלת מימדית.
בתלת מימד, הטורבולנציה שואבת ארגיה מזרימות בקנה מידה גדול ומעבירה אותה לתוך מערבולות קטנות, שבתורן מעבירות אותה למערבולות קטנות עוד יותר. בסופו של דבר, מגיעים לקנה מידה שבו הדיסיפציה היא יעילה. בדו מימד, לעומת זאת, המערבולות נסכמות והאנרגיה מועברת לקנה מידה גדול יותר. תופעה זו, הקרויה "אשדת אנרגיה הפוכה", התגלתה על ידי רוברט קריצ'נן, וכתוצאה מתופעה זו נוצרת זרימה גדולה ויציבה.
בלימודי הפוסט דוקטורט שלה, חקרה פרופ' פרישמן תופעה זו של סידור עצמי של ערורים אקראיים של נוזל. אם חיכוך הנוזל עם קרקעית המכל שבו הוא נמצא מופחת משמעותית, בסופו של דבר מתפתחת זרימה קוהרנטית גדולה. סביר היה להניח כי מאפייני הזרימה אינם תלויים בתכונות המסוימות של הכוחות אשר עררו את הנוזל בסקאלות קטנות. במחקרה, סייעה פרופ' פרישמן בפיתוח תאוריה שהסבירה כיצד הזרימה מוגדרת באופן שנקבע בצורה סגורה, וכן סייעה בהבנת אופי התנודות הקטנות שמתווספות לזרימה זו. תאוריה זו היא התאוריה העקבית הראשונה, העוסקת באינטרקציה בין הזרימה הקוהרנטית וטורבולנציה. הרחבת התיאוריה לתלת מימד, כדי שתכלול זרימה בצינורות או שכבה גבולית באטמוספירה, עדיין נשארת אתגר לעתיד. לתיאוריה הזו ייתכנו שימושים מעשיים רבים.
נושא נוסף עליו עבדה פרופ' פרישמן בלימודי הפוסט דוקטורט שלה, ועודנו ממשיך להיות נושא המחקר שלה היום, הוא חקר דינמיקה של חלקיקים במצב של ריסון יתר, בנוכחות רעש מהסביבה. במצב של ריסון יתר, החיכוך עם התמיסה שבה נמצאים החלקיקים משמעותי הרבה יותר מהתנע של החלקיקים. בדרך כלל, זה המצב כאשר מימדי החלקיקים הם קטנים, והוא מתאים למספר ריינולדס קטן.
לדוגמה, עבור חלקיקים שגודלם בסדר גודל של מיקרון, הפלוקטואציות התרמיות שהם מרגישים משמעותיות. ואכן, התנגשויות עם מולקולות התמיסה ללא נוכחות כוחות נוספים גורמות לחלקיקים לבצע תנועה בראונית כתוצאה מכוח אקראי לבן שפועל עליהם. לכן, כוחות אחרים הפועלים על החלקיקים, אשר יכולים לנבוע מהתנגשויות עם חלקיקים אחרים או כוחות חיצוניים כלשהם, ממוסכים על ידי כוחות אקראיים האלה. שאלת המחקר של פרופ' פרישמן הייתה: האם הכוחות הדטרמיניסטיים יכולים להיות מחושבים ממסלולי החלקיקים בלבד?
אם נסתכל באופן כללי יותר, דינמיקה כזו נקראת דינמיקה בראונית ומהווה מודל בסיסי להתפתחות בזמן של מערכות עם דרגות חופש מהירות שיכולות להיות מיוצגות בתור רעש לבן. למודל מסוג זה קיימים שימושים בכלכלה, דינמיקת אקלים וביולוגיה.
פרופ' פרישמן הקבילה מערכות מסוג זה לתורת הממסר, היכן שהאות מקודד, מועבר דרך ערוץ רועש ולבסוף נקרא על ידי הנמען. במקרה שלנו, ההודעה היא הכוח, והקידוד הוא מדידת כוח זה לאורך מסלול החלקיק. הרעש בערוץ הוא הרעש הלבן שמתווסף לכוח שפועל על החלקיק.
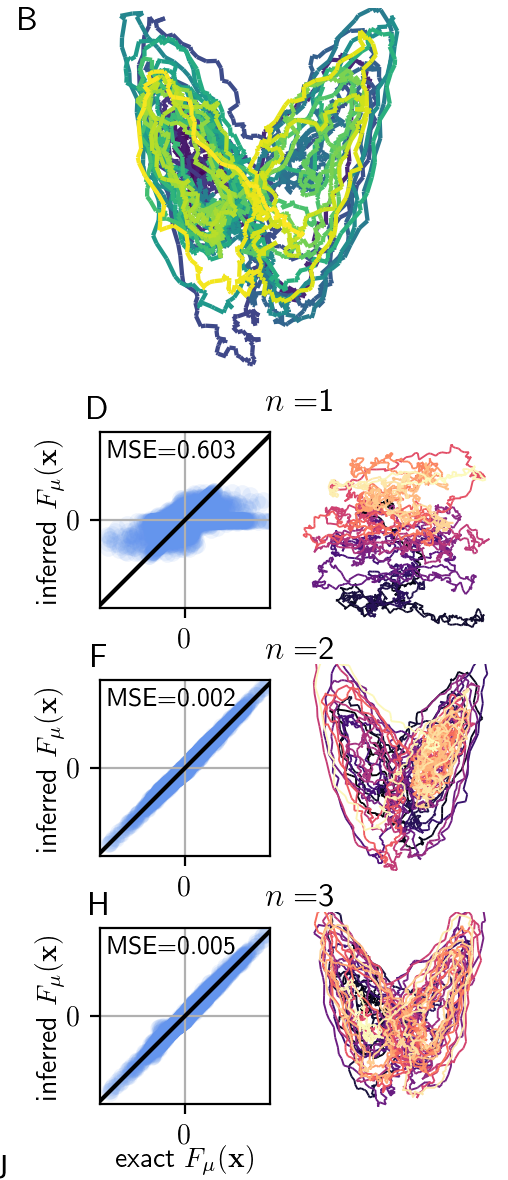
פרופ' פרישמן פיתחה מסגרת תיאורטית המאפשרת לחשב כוח זה, תוך שימוש ברעיון הגורס כי עבור כל מסלול סופי קיימת כמות סופית של אינפורמציה המתארת אותו. המסגרת התיאורטית כוללת רגרסיה חלקה של שדה הכוח תוך שימוש בפונקציות ידועות, כאשר התאמת יתר ותת-התאמה שתיהן נשלטות בהתבסס על האינפורמציה שבפירוק הכוח. האנלוגיה שבין הדיסיפציה במערכות אלה ותורת המססר הינה קונספט חדש ומעניין.
Ronceray and Frishman, PRX (2020)
המסגרת התיאורטית הזו יכולה להיות שימושית עבור מדענים המבצעים ניסויים על חלקיקים אקטיביים עם כוח מניע פנימי וכן אינטרקציות בין חלקיקיות. באופן כללי יותר, ניתן לעשות בה שימוש עבור מגוון רחב של מערכות סטוכסטיות היכן שיש עניין בבניית מודל עבור הדינמיקה מתוך מידע רועש ומוגבל.
הבעיות שפרופ' פרישמן מתעניינת בהם במחקרה משלבות דינמיקה לא ליניארית וסטטיסטיקה. מטרתה המרכזית היא למצוא האם קיימים עקרונות מנחים, או פורמליזם מתמטי לתיאור מערכות מחוץ לשיווי משקל, ובפרט להבין טוב יותר את תפקיד הדינמיקה בהן. כמה מהשימושים המשמעותיים ביותר של הבנה זו הם ניתוח זרימה טורבולנטית ומערכות ביולוגיות.
וכמובן, להיות מדען לא רק אומר לחלום מדע, אלא גם להיות סקרן לדעת יותר על תופעות מחיי היומיום.
על מנת להמחיש נקודה זו, נספר כי פרופ' פרישמן מתעניינת גם בדינמיקה לא ליניארית של בועת סבון גלילית, אשר כאשר מושכים אותה לצדדים, מתפוצצת ויוצרת בועה קטנה במרכז. שאלת המחקר בנושא זה היא – כיצד גודל הבועה הקטנה קשור למהירות המשיכה, כאשר לוקחים בחשבון את הזרימה שבתוך הבועה ואת מתח הפנים.

עולם הדינמיקה מחוץ לשיווי משקל והטורבולנציה הוא עולם מרתק ומלא בשאלות פתוחות. המסע למציאת התשובות איננו נגמר לעולם, ואתם מוזמנים להצטרף אליו.